这么抽象的定理都能理解,学高数就没有问题了,上下极限充要条件

前面老黄介绍过有界数列上、下极限的ε-N充要条件. 其实有界数列的上、下极限的充要条件可以有许多，比如还有另一个充要条件是与有界数列的上下确界有关的。

这个定理知识的人并不多，而有一些了解的小伙伴，又很容易对它产生误解。错误地以为，有界数列的上确界就是上极限，下确界就是下极限。其实完全不是酱纸的。

记数列{xn}的上确界为an，然后去掉第一项，得到数列{x_(n+1)}, 它的上确界记为a_(n+1), 再去掉第二项，……，依此类推，会得到一个上确界数列sup(k>=n){xk}, 各项为a_(n+1), a_(n+2),…,a_(n+n),… 而这个上确界数列的极限就是上极限。很明显的，在确得上确界数列各项时，每一项都会去掉原数列的一个项，总有一个项是原数列的上确界，因此，原数列的上确界并不是上极限。讲明白这个道理，接下来老黄给大家证明上、下极限的这个与确界有关的充要条件。

设{xn}为有界数列，则

1、ˉA为{xn}上极限的充要条件是：ˉA=lim(n→∞)sup(k≥n){xk}；

2、▁A为{xn}下极限的充要条件是：▁A=lim(n→∞)inf(k≥n){xk}.

证：1、[必要性] 设lim ?(n→∞)xn=ˉA(ˉA为有限值), 则

?ε>0，{xn}中大于ˉA+ε的项至多有限个，设其中下标最大者为N，【这是利用上极限的ε-N充要条件来证明】

则当n≥N+1时，xn≤ˉA+ε, ∴sup(k≥N+1){xk}≤ˉA+ε,

又{xn}中大于ˉA-ε的项有无限多个，∴对一切n有sup(k≥n){xk}>ˉA-ε.【这是极限的ε-N定义条件】

∴当n>N时，有ˉA-ε【这里也可以用极限的迫敛性来理解】

∴lim(n→∞)sup(k≥n){xk}=ˉA.

[充分性] 设lim(n→∞)sup(k≥n){xk}=ˉA(ˉA为有限值),

设An=sup(k≥n){xk}，则{An}递减，【上确界数列递减，因为是从前面去掉原数列的项，所以剩余部分有可能被剔除了原数列的上确界，即最大值，原来的最大值被去掉了，新的最大值自然只可能变小或不变了】

∴ˉA=inf{An}，即?ε>0，存在N，使AN<ˉA+ε,【这是上确界的定义】

∴当n≥N时，xn<ˉA+ε,【上确界都比ˉA+ε小，普通项就更小了】

即{xn}中大于ˉA+ε的项至多有限个；【只有下标为N以下的项可能大于ˉA+ε】

又对一切n有An≥ˉA>ˉA-ε,∴{xn}中大于ˉA-ε的项有无限个，【这是上极限的ε-N充要条件】

∴lim ?(n→∞)xn=ˉA.

2、由1有 lim ?(n→∞)(-xn)=lim(n→∞)sup(k≥n){-xk}=-lim(n→∞)inf(k≥n){xk},【利用1的结论，取相反数列，再根据上确界等于相反数列的下确界的相反数得证】

又lim ?(n→∞)(-xn)=-▁lim(n→∞)xn=-▁A，∴▁A=lim(n→∞)inf(k≥n){xk}.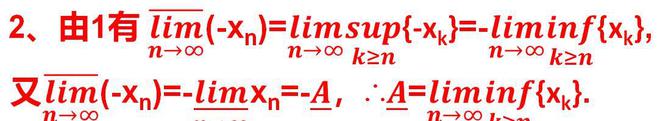

像这么抽象的定理你要是都能理解，那么学高数就没有什么问题了。